我们的解析器已经可以处理基本的加减乘除运算并支持括号了。但是随着功能越来越多，可能出现的错误也越来越多。不重视错误处理的话，碰到非法的表达式时会出现什么结果，我们完全是无法预料的。所以本章就打个岔，给解析器加上一套错误处理逻辑。这知识和编译原理关系不大，不感兴趣的朋友可以略过。

本章还会顺带聊一聊负数的解析，用递归的方式处理负数可以做的很简单，想复杂点也可以做的很复杂。如果是用调度场算法处理表达式中的负数的话，推荐看看这一篇文章（英文），我就不深入分析了。负数解析不涉及到编译原理相关的新知识，不感兴趣也可以略过。

错误处理

想要把正在解析的表达式，和解析中遇到的错误配对关联起来，在C语言里当然是用结构体最方便啦：

typedef struct {
    const char *expStr;
    int errType;
} slm_expr;

然后我们要对现在的代码做修改，把所有传递const char **expStr参数的地方改成传递slm_expr *e，当然函数体里代码也要做对应的修改。

是不是有点熟悉？ObjC里的objc_msgSend就是这么玩的，python等部分语言里也是把self当做类成员函数的第一个参数。

做完了准备之后我们就要开始错误处理了，以number函数为例，我们需要在出现不期望字符时报错：

int number(slm_expr *e)
{
    if (*e->expStr < '0' || *e->expStr > '9') {
        e->errType = SLM_EXPRESSION_ERROR_TYPE_EXPECT_DIGIT;
        return 0;
    }
    int result = *e->expStr - '0';
    (e->expStr)++;
    return result;
}

可以看到我们报错的手段就是在结构体里把errType标记成对应的错误，然后立刻终止解析。当然只终止当前函数的解析是不够的，上层函数发现下层函数解析出错了，应该递归的终止解析。我们以expr函数为例：

int expr(slm_expr *e)
{
    int result = term(e);
    if (e->errType) return 0;
    while (*e->expStr == '+' || *e->expStr == '-') {
        char op = *e->expStr;
        (e->expStr)++;
        int t = term(e);
        if (e->errType) return 0;
        if (op == '+') {
            result += t;
        } else {
            result -= t;
        }
    }
    return result;
}

可以看到每次在调用term函数后，我们都需要判断下它有没有设置过errType，有的话就需要递归终止解析。当然大家会发现，对errType的操作都是比较固定的模式，所以我们用个宏定义来让代码看上去简洁点：

1 2	#define TRY(func) func; if (e->errType) return 0; #define THROW(error) e->errType = error; return 0;

用宏定义替换完代码后，我们的错误处理差不多就做完了，完整代码参照SlimeExpressionC-chapter3.1。不得不说没有提供try...catch...语法的语言写错误处理是多么的蛋疼😂，如果是用高级语言那么这段逻辑会优雅很多。当然用goto语句来实现错误处理也是可行的，但是一是难以阅读，二是容易玩脱，感兴趣的朋友可以自己试试。

负号解析

负号的优先级是怎样的？我们来先看一个截图：

05-A

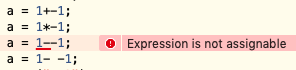
可见在常见的C语言编译器里面，负数出现在表达式中间是可以的，且负号优先级是比乘除法还高的。

关于C语言里运算符的优先级，大家可以参考这一篇文章：C运算符优先级

第三行炸了是因为后缀自减运算符优先级是最高的，所以--被识别成了自减运算符。而自减运算符是不能应用在常量上的，所以出现了编译错误。其实像第四行一样用空格把两个减号断开一下，就又可以正常编译了。

我在解析器里就不打算支持自增自减运算符了，因为我个人十分讨厌人问我a---a到底该解析成什么，所以从根源上杜绝这个问题。😜

为什么C语言要设计成这样呢？其实是因为这样的设计，对于文法和递归解析来说是最容易的。按照这样的设计，负号应该是数字解析中的一部分，所以我们把解析数字用的文法改进成这样：

1 2	number -> '-' digit \| digit digit -> '0' \| '1' \| '2' \| '3' \| '4' \| '5' \| '6' \| '7' \| '8' \| '9'

这个逻辑十分简单，我们就不需要把它拆成两个函数来写了，事实证明写在一个函数里会更简洁些：

int number(slm_expr *e)
{
    int hasMinus = 0;
    if (*e->expStr == '-') {
        (e->expStr)++;
        hasMinus = 1;
    }
    if (*e->expStr < '0' || *e->expStr > '9') {
        THROW(SLM_EXPRESSION_ERROR_TYPE_EXPECT_DIGIT);
    }
    int result = *e->expStr - '0';
    (e->expStr)++;
    if (hasMinus) {
        result *= -1;
    }
    return result;
}

是的，支持负数只需要改这么一个函数，完整的代码参照：SlimeExpressionC-chapter3.2

负号的深入探讨

上一小节提到的文法是解析负数的最简单文法，那么复杂点的场景要怎么处理？

我们举个例子：

1+-1，1--1这类写法总归不太符合正常习惯
-1+1，-1-2，1-(-1)这类写法就正常些

总结起来就是，负号应该只出现在一个表达式（expr）的首个数字里。如果想要实现这样的功能，我们的文法要怎么设计呢？那可麻烦了去了……

在递归逻辑里，如果想要记住一个状态，那么只能一步步的把状态传递下去，一种方式就是用文法进行传递，那么文法大概会设计成这么个样子：

expr        -> firstTerm {'+' term | '-' term}
firstTerm   -> fisrtFactor {'*' factor | '/' factor | '%' factor}
term        -> factor {'*' factor | '/' factor | '%' factor}
fisrtFactor -> fisrtNumber | '(' expr ')'
factor      -> number | '(' expr ')'
firstNumber -> '-' digit | digit
number      -> digit
digit       -> '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'

003

看我的表情……每一级向下传递都得多写一个产生式，我们现在的文法才这么简单就直接产生式数量double了，以后出现了函数解析、变量名解析之类的还不得原地爆炸？不敢想不敢想。

当然还有另一种方式，就是通过context传递状态。在面向对象的语言里那就是通过实例的属性/成员变量去传递状态，在我们的C代码里那就是给结构体再加一个布尔值变量isFisrtNumber咯。

具体的做法就是在进入expr函数时，把isFisrtNumber置为true，在解析完第一个数字后，再把isFisrtNumber置为false，只有在isFisrtNumber为true的时候，解析数字才支持以负号开始。

等等，那万一以后我们支持变量了，i+-1里的-1的确是第一个数字啊，这时候咋办？改代码呗，第一个变量解析完之后也把isFisrtNumber置为false。

等等，那万一以后我们支持函数了，f(1)+-1里的-1好像也有问题啊，咋办？再改……

等等，那expr是会嵌套解析的，我们要不要搞一个堆栈记录每一层的isFisrtNumber？……

002

总之，各种各样的问题会接踵而至，就是这样喵。所以呢，大家应该也明白了为什么我说上一小节提到的文法是解析负数的最简单文法。感兴趣的同学可以自己试试实现这种复杂的负号解析逻辑，我这里就不尝试实现了。今天的入门课也就到这里，希望可以拓宽一下大家的思路。

其它章节

（三）简单错误处理逻辑以及负数的解析

001

编译原理入门课：（三）简单错误处理逻辑以及负数的解析

错误处理

负号解析

负号的深入探讨

其它章节