之前为了快速进入主题，我们约定了表达式里只会出现个位数的数字。现在是时候打破这个规则，支持多位数的数字了。为了支持这点，我们就需要接触一个新的步骤——词法分析。

词法分析的作用

词法分析就是把一个完整的语句拆分成一个个词（token），方便之后进行进一步的语法分析。

举个简单的例子：今天真热，将会被拆分成<今天>, <真>, <热>。当然拆分成<今>, <天真>, <热>也是一种可能，但是这样的分词方式不符合汉语的语法。

好在计算机语言大部分是英文的，词与词之间一般用空白符隔开，很容易拆分。举个代码的例子：a = 1.1 + 2将被拆分为<id: a>, <等号>, <浮点数: 1.1>, <加号>, <整数: 2>，当然我们也可以把加号和等号都算作运算符，做一定的聚合得到<id: a>, <运算符: =>, <浮点数: 1.1>, <运算符: +>, <整数: 2>。

有人要问为什么拆分token的逻辑要做成单独的词法分析步骤，而不是放在语法分析里一起做？这是个好问题，还真的有点难回答。从我个人的观点来说主要的两点可能是：

词法分析不太适于用递归的方式来解析，性能会比较低，也不方便为不同种类的token写特有的解析逻辑
词法分析作为单独的步骤，可以更方便独立的为token附加各种属性，为后续的步骤做准备

要问得更具体的话，还是建议各位在自己写编译器的过程中自行体会一下……😂

上面也提到了词法分析器主要是用来拆分token的，但是词法分析器还要负责一些别的工作。我们总结下词法分析器的主要工作范围：

拆分token。
过滤掉多余的空白符，发现无法识别的无效字符并报错。
记录代码中每个token的位置信息，方便在编译出错时可以定位到具体的位置。
宏定义处理。
和符号表进行交互。例如定义函数时把函数名加入函数表，方便重复定义同名函数时进行报错。

我准备一开始做的简单点，先把必备的前两条功能给实现了。

词法分析的实现

定义要用到的结构体和枚举

首先我们得定义一个用来描述token的结构体：

typedef struct {
    int type;
    int value;
} slm_token;

关于token的类型，前文也提到了，运算符可以做一定聚合，也可以每种运算符算一种类型。我这里就不做聚合了，把我们前文出现过的token类型都定义出来：

enum {
    SLM_EXPRESSION_TOKEN_UNKNOWN = 0,
    SLM_EXPRESSION_TOKEN_DIGITS,
    SLM_EXPRESSION_TOKEN_ADD,
    ...
    SLM_EXPRESSION_TOKEN_CLOSE,
    SLM_EXPRESSION_TOKEN_END
};

然后扩展下我们的slm_expr结构体，以后语法分析器就不应该直接读expStr而应该从token里取值啦：

typedef struct {
    const char *expStr;
    slm_token token;
    int errType;
} slm_expr;

词法分析核心实现及状态机

词法分析的核心函数一般叫做next或者scan，我们这里就叫它next吧。它主要实现的功能是读取下一个有效的token，存到slm_expr结构体的token成员里以供语法分析器使用。

C语言的词法分析十分简单，因为根据token的首字符就能区分出token的类型：如果首字符是数字那一定是个数值token；如果首字符是字母或下划线那一定是个id类的token，至于这个id是关键字还是函数名、变量名那就另说了。怎么样？是不是突然明白了大部分计算机语言里变量名不能以数字开头的原因？

这一章里面我们暂时还用不到id类的token，所以主要讲一下数值token的处理：

void next(slm_expr *e) {
    ...
    if (isdigit(*e->expStr)) {
        e->token.type = SLM_EXPRESSION_TOKEN_DIGITS;
        e->token.value = *e->expStr - '0';
        (e->expStr)++;
        while (isdigit(*e->expStr)) {
            e->token.value = e->token.value * 10 + (*e->expStr - '0');
            (e->expStr)++;
        }
    }
    ...
}

可见如果发现一个token是以数字开头的，那么我们可以循环读取后面连续的数字，直接把整个token完整的数字值读取出来，供语法分析器在后面的分析中使用。

词法分析的过程一般可以用状态机来描述，上面的解析过程对应的状态机可以用这么个图来表示：

09-A

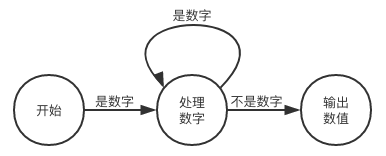
可以看出来这种图和流程图相似，更适合用条件分支及循环语句来实现它的逻辑。然后我们可以大致的补全一下整个词法分析器的状态机图：

09-B

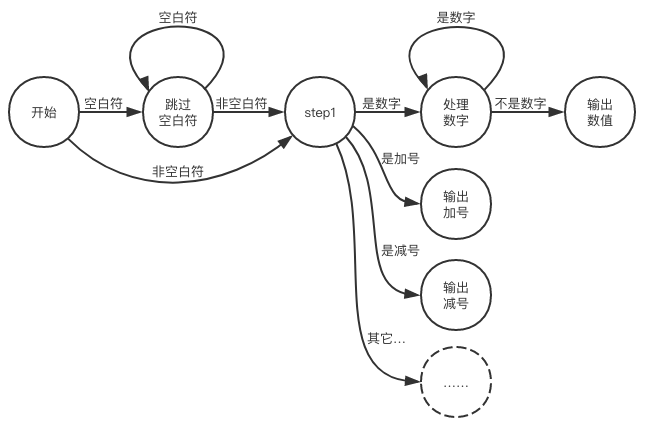
接下来照着状态机图来实现代码逻辑就好了，在这里不贴完整代码了。注意如果出现了用状态机无法描述的token，那么这一定是个非法的token。

用状态机图可以直观的表示词法分析的流程，以后扩展数值类型支持浮点数之类的，都可以从画状态机图开始。比如大部分计算机语言支持的数字类型，可以用下面的状态机图来表示（图片来自Online JSON Viewer）：

09-C

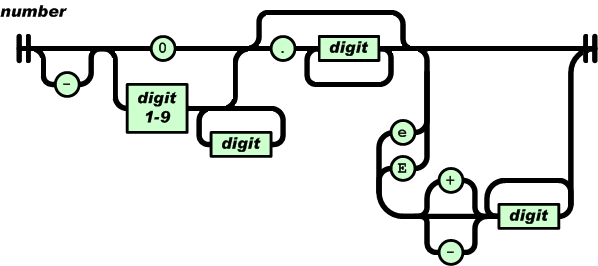
除了状态机，另一个超级适于描述词法分析器的就是正则表达式，有兴趣的同学可以自行去了解下。著名的词法分析器Lex就是用正则表达式描述词法规则的。

给语法分析器接入词法分析器

以最典型的number函数为例：

int number(slm_expr *e)
{
    int hasMinus = 0;
    if (e->token.type == SLM_EXPRESSION_TOKEN_SUB_OR_MINUS) {
        TRY(next(e));
        hasMinus = 1;
    }
    if (e->token.type != SLM_EXPRESSION_TOKEN_DIGITS) {
        THROW(SLM_EXPRESSION_ERROR_EXPECT_DIGIT);
    }
    int result = e->token.value;
    TRY(next(e));
    if (hasMinus) {
        result *= -1;
    }
    return result;
}

我们把之前从e->expStr直接取值的代码都换成读取e->token。还要把(e->expStr)++的地方都替换为TRY(next(e))，加上TRY是因为next里面也会报非法token的错误。当然不能忘记的是，在main函数里必须预先调用一次next，不然首次进入语法解析器的时候e->token会是空的。

把所有语法分析步骤里的代码替换完之后，我们就可以得到一个能剔除空格、识别非法字符和多位数字的解析器啦。完整的代码我就不在这里全贴出来了，存放在SlimeExpressionC，欢迎大家自取。